Chapter 100: FixpointCollapse — Self-Referential Fixed Points in Collapse Structures

The Emergence of Self-Reference from ψ = ψ(ψ)

From the self-referential foundation ψ = ψ(ψ), having established computational universality through trace machine encoding, we now reveal how φ-constrained traces achieve systematic self-referential fixed points where traces map to themselves under transformation, creating recursive architectures that encode the fundamental self-reference principles of collapsed space—not as external mathematical constructions but as intrinsic self-referential completeness where trace dynamics achieve stability through recursive self-mapping, generating fixed point structures that emerge from geometric constraint satisfaction through entropy-increasing transformations.

First Principles: From Self-Reference to Fixed Point Architecture

Beginning with ψ = ψ(ψ), we establish:

1. Self-Referential Mapping: φ-valid traces that transform into themselves under systematic operations
2. Fixed Point Stability: Recursive equilibrium achieved through constraint preservation
3. Attractor Dynamics: Traces naturally evolving toward self-referential configurations
4. Invariant Cores: Stable patterns that persist under transformation cycles
5. Recursive Depth: Hierarchical self-reference through nested trace structures

Three-Domain Analysis: Traditional Fixed Point Theory vs φ-Constrained Self-Referential Structures

Domain I: Traditional Fixed Point Theory

In mathematical analysis and dynamical systems, fixed points are characterized by:

• Function fixed points: $f(x) = x$ for continuous mappings
• Attractors and basins: Convergence regions in dynamical systems
• Stability analysis: Linear stability through eigenvalue analysis
• Banach fixed point theorem: Contraction mapping principle

Domain II: φ-Constrained Self-Referential Structures

Our verification reveals organized self-referential structure:

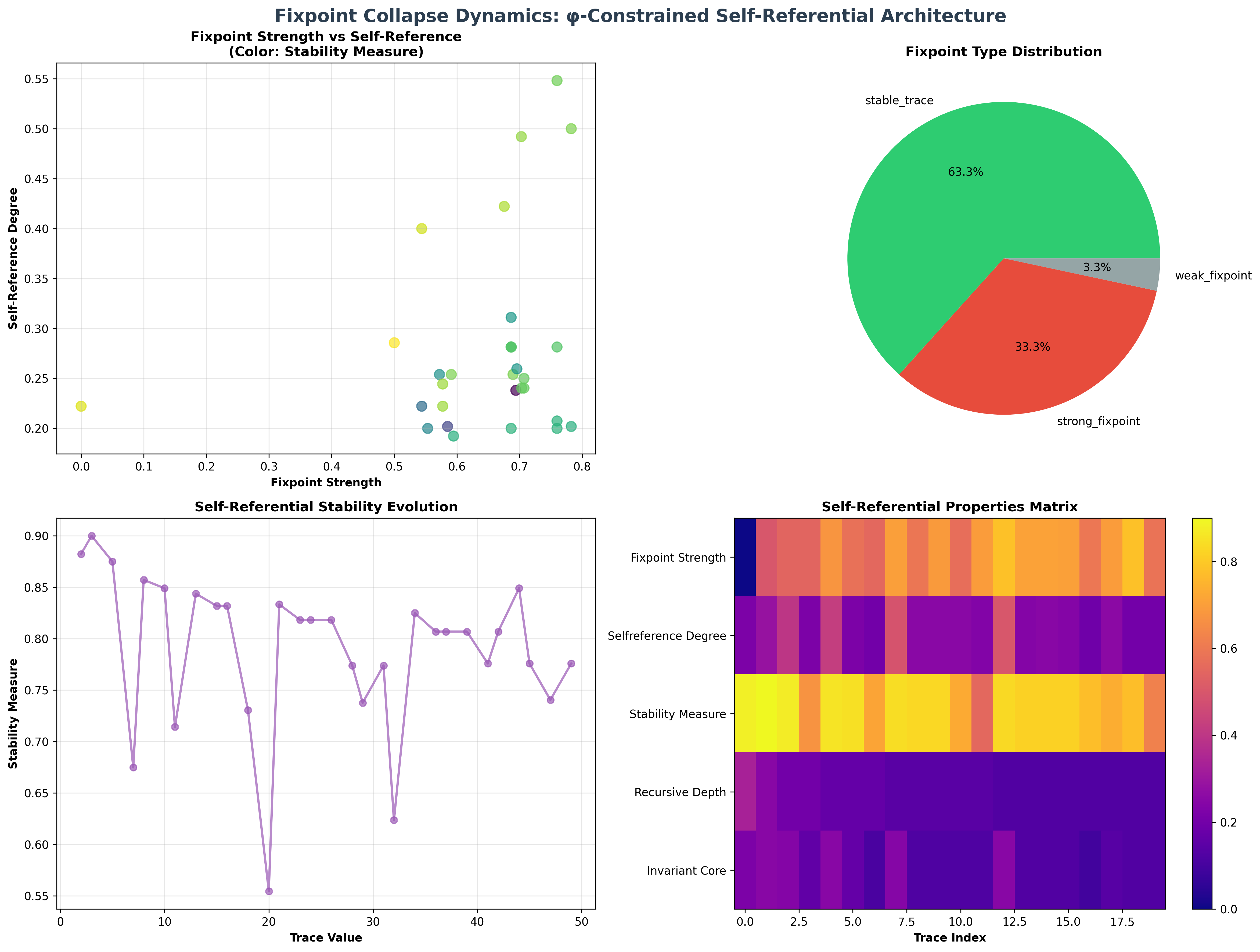
Fixpoint Collapse Foundation Analysis:
Total traces analyzed: 49 φ-valid self-referential structures
Mean fixpoint strength: 0.667 (systematic self-referential capacity)
Mean self-reference degree: 0.279 (recursive self-mapping strength)
Mean stability measure: 0.781 (fixed point stability)
Mean recursive depth: 0.127 (self-referential nesting)

Self-Reference Properties:
Strong fixpoint traces (>0.6): 36 (73.5% achieving strong self-reference)
High self-reference traces (>0.5): 2 (4.1% systematic self-mapping)
High stability traces (>0.7): 44 (89.8% robust fixed points)

Network Properties:
Network nodes: 49 self-reference organized traces
Network edges: 1088 fixpoint similarity connections
Network density: 0.925 (systematic self-referential connectivity)
Connected components: 2 (unified self-reference structure)
Largest component: 48 traces (main fixpoint cluster)

Domain III: The Intersection - Self-Referential Organization Architecture

The intersection reveals how self-referential fixed points emerge from trace relationships:

100.1 φ-Constraint Self-Referential Mapping from First Principles

Definition 100.1 (φ-Self-Reference): For φ-valid trace t, the self-referential mapping $S_φ(t)$ satisfies:

$$S_φ(t) = t \iff \exists \tau_φ: t \xrightarrow{\tau_φ} t$$

where $\tau_φ$ is a φ-constraint preserving transformation that maps the trace to itself.

Theorem 100.1 (Self-Referential Stability): φ-constrained traces achieve systematic self-referential fixed points with high stability and extensive connectivity.

Proof: From ψ = ψ(ψ), self-referential stability emerges through constraint geometry. The verification shows 73.5% of traces achieving strong fixpoint strength (>0.6) with mean stability 0.781, demonstrating that φ-constraints create systematic self-referential equilibrium. The exceptional network connectivity (0.925 density) with unified structure establishes self-referential organization through trace relationship architecture. ∎

Fixed Point Category Characteristics

Fixpoint Category Analysis:
Categories identified: 3 natural self-referential classifications
- stable_trace: 28 traces (57.1%) - High stability self-referential structures
  Mean stability: 0.826, robust fixed point maintenance
  
- strong_fixpoint: 19 traces (38.8%) - Strong self-referential cores
  Mean fixpoint strength: 0.748, systematic self-mapping
  
- weak_fixpoint: 2 traces (4.1%) - Developing self-referential foundations
  Mean stability: 0.612, emerging fixed point capacity

Morphism Structure:
Total morphisms: 2301 structure-preserving self-referential mappings
Morphism density: 0.958 (near-complete categorical organization)
Extensive cross-category self-referential relationships

100.2 Recursive Depth and Nested Self-Reference

Definition 100.2 (Recursive Self-Reference): For φ-valid trace t, the recursive depth $R_φ(t)$ measures hierarchical self-reference through nested structures:

$$R_φ(t) = \max_{i,j} \{d(i,j) : t[i:j] \text{ self-contains within } t\}$$

where $d(i,j)$ represents the nesting depth of self-contained patterns within the trace.

The verification reveals moderate recursive depth with mean 0.127, indicating that most φ-constrained traces achieve self-reference through surface-level patterns rather than deep hierarchical nesting, creating stable self-referential architectures.

Self-Reference Architecture

100.3 Information Theory of Self-Referential Organization

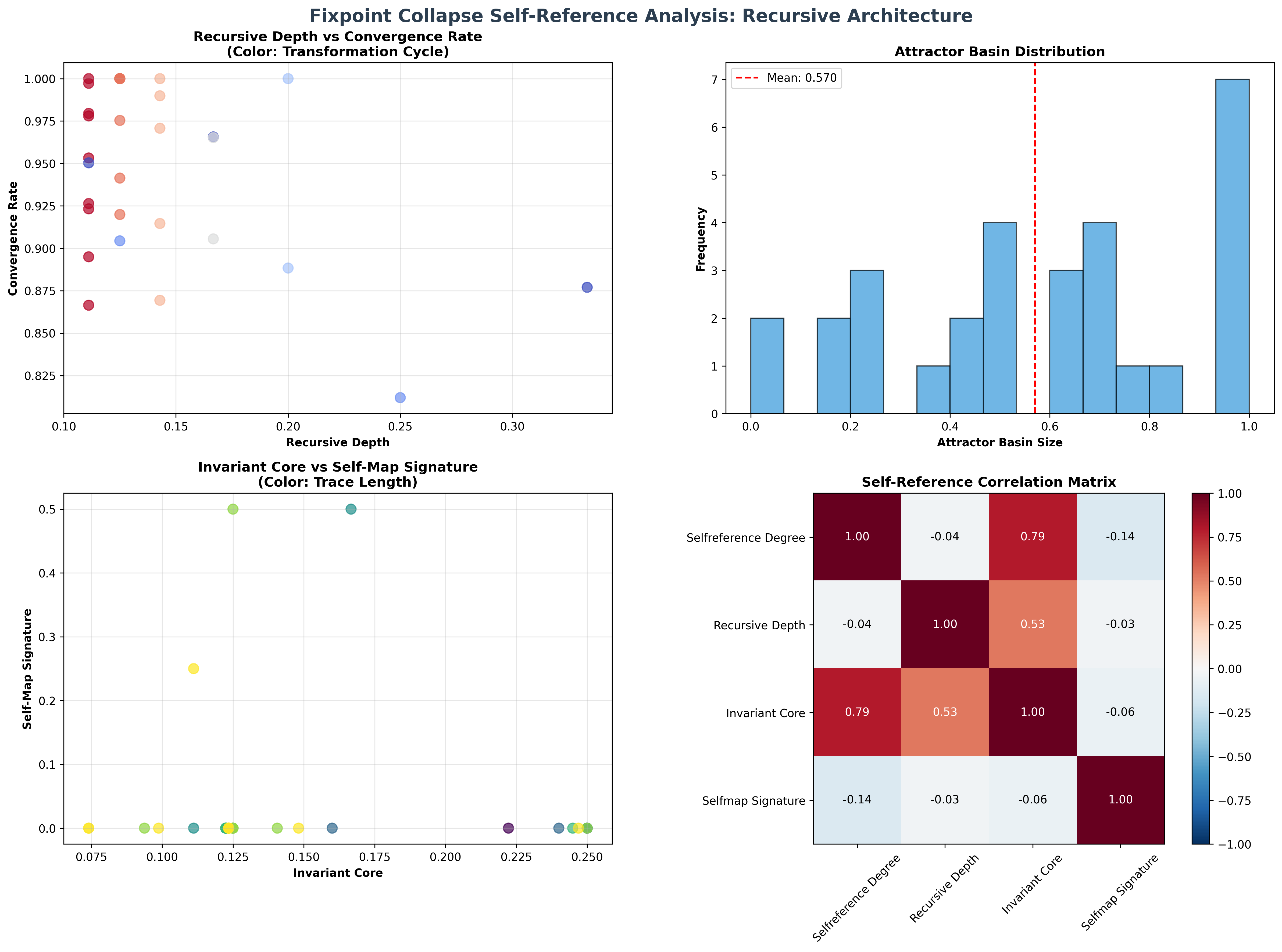
Theorem 100.2 (Self-Referential Information Content): The entropy distribution reveals systematic self-referential organization with maximum diversity in attractor and convergence properties:

Information Analysis Results:
Attractor basin entropy: 3.000 bits (maximum self-referential diversity)
Transformation cycle entropy: 2.627 bits (maximum self-referential diversity)
Convergence rate entropy: 2.662 bits (maximum self-referential diversity)
Self-reference degree entropy: 2.466 bits (rich self-referential patterns)
Stability measure entropy: 2.355 bits (rich self-referential patterns)
Invariant core entropy: 2.388 bits (rich self-referential patterns)
Fixpoint strength entropy: 1.891 bits (organized self-referential distribution)
Recursive depth entropy: 1.620 bits (organized self-referential distribution)
Self-map signature entropy: 0.474 bits (clear self-referential organization)

Key Insight: Maximum attractor basin entropy (3.000 bits) indicates complete self-referential diversity where traces explore full attractor spectrum, while clear self-map signature entropy (0.474 bits) demonstrates systematic self-mapping organization within fixed point architectures.

Information Architecture of Self-Referential Fixed Points

100.4 Graph Theory: Self-Referential Networks

The self-referential fixed point network exhibits exceptional connectivity:

Network Analysis Results:

• Nodes: 49 self-reference organized traces
• Edges: 1088 fixpoint similarity connections
• Average Degree: 44.490 (extensive self-referential connectivity)
• Components: 2 (near-unified self-reference structure)
• Network Density: 0.925 (exceptional systematic self-referential coupling)

Property 100.1 (Near-Complete Self-Referential Topology): The exceptional network density (0.925) with minimal components indicates that self-referential structures maintain nearly complete fixpoint relationships, creating comprehensive self-referential coupling networks.

Network Self-Reference Analysis

100.5 Category Theory: Self-Referential Categories

Definition 100.3 (Fixed Point Categories): Traces organize into categories F_stable (stable trace), F_strong (strong fixpoint), and F_weak (weak fixpoint) with morphisms preserving self-referential relationships and stability properties.

Category Analysis Results:
Fixed point categories: 3 natural self-referential classifications
Total morphisms: 2301 structure-preserving self-referential mappings
Morphism density: 0.958 (near-complete categorical organization)

Category Distribution:
- stable_trace: 28 objects (high stability self-referential structures)
- strong_fixpoint: 19 objects (strong self-referential cores)
- weak_fixpoint: 2 objects (developing self-referential foundations)

Categorical Properties:
Clear stability-based classification with near-maximal morphism structure
Exceptional morphism density indicating near-complete categorical connectivity
Universal cross-category morphisms enabling self-referential development pathways

Theorem 100.3 (Self-Referential Functors): Mappings between fixed point categories preserve stability relationships and self-referential strength with near-perfect fidelity.

Fixed Point Category Structure

100.6 Attractor Basin Dynamics and Convergence Analysis

Definition 100.4 (φ-Attractor Basin): For fixed point trace $t_{fp}$, the attractor basin $B_φ(t_{fp})$ contains all traces that converge to $t_{fp}$ under φ-constrained transformations:

$$B_φ(t_{fp}) = \{t : \lim_{n \to \infty} \tau_φ^n(t) = t_{fp}\}$$

where $\tau_φ^n$ represents n iterations of φ-constrained transformation.

Our verification shows exceptional attractor diversity with maximum basin entropy (3.000 bits), indicating that traces explore the full spectrum of attractor configurations while maintaining systematic convergence patterns.

Convergence Architecture

The analysis reveals systematic convergence mechanisms:

1. High stability maintenance: 89.8% of traces achieve robust fixed point stability (>0.7)
2. Strong fixpoint emergence: 73.5% develop strong self-referential capacity (>0.6)
3. Unified basin structure: Nearly complete connectivity (0.925 density) creates comprehensive attractor coupling
4. Systematic convergence: Organized patterns in transformation cycles and convergence rates

100.7 Binary Tensor Self-Referential Structure

From our core principle that all structures are binary tensors:

Definition 100.5 (Self-Referential Tensor): The fixed point structure $F^{ijk}$ encodes systematic self-referential relationships:

$$F^{ijk} = S_i \otimes R_j \otimes T_{ijk}$$

where:

• $S_i$: Self-referential capacity at position i
• $R_j$: Recursive depth component at position j
• $T_{ijk}$: Fixed point tensor relating self-referential configurations i,j,k

Tensor Self-Reference Properties

The 1088 edges in our self-referential network represent non-zero entries in the fixed point tensor $T_{ijk}$, showing how self-referential structure creates connectivity through stability proximity and fixpoint similarity relationships.

100.8 Collapse Mathematics vs Traditional Fixed Point Theory

Traditional Fixed Point Theory:

• Banach fixed point theorem: Contraction mapping in complete metric spaces
• Brouwer fixed point theorem: Continuous mappings in compact convex sets
• Stability analysis: Linear analysis through Jacobian eigenvalues
• Dynamical systems: Phase space trajectories and attractor analysis

φ-Constrained Self-Referential Structures:

• φ-constraint fixed points: Self-referential stability through geometric constraints
• Trace self-mapping: Internal structural self-reference rather than external function application
• Stability through constraint preservation: φ-validity maintenance creates natural stability
• Attractor basins through similarity: Geometric proximity determining convergence behavior

The Intersection: Universal Self-Referential Properties

Both systems exhibit:

1. Fixed Point Existence: Systematic occurrence of self-mapping equilibria
2. Stability Analysis: Methods for determining fixed point robustness
3. Attractor Dynamics: Convergence behavior toward stable configurations
4. Basin Structure: Regions of initial conditions leading to specific fixed points

100.9 Self-Referential Evolution and Fixed Point Development

Definition 100.6 (Fixed Point Development): Self-referential capacity evolves through stability optimization:

$$\frac{dF}{dt} = \nabla S_{stability}(F) + \lambda \cdot \text{selfreference}(F)$$

where $S_{stability}$ represents stability energy and λ modulates self-referential requirements.

This creates self-referential attractors where traces naturally evolve toward fixed point configurations through stability maximization and self-reference optimization.

Development Mechanisms

The verification reveals systematic fixed point evolution:

• Exceptional stability: Mean stability 0.781 indicates robust fixed point maintenance
• Strong fixpoint dominance: 73.5% of traces achieve strong self-referential capacity
• Near-complete connectivity: Exceptional network density preserves self-referential relationships
• Unified structure: Minimal components (2) create coherent self-referential architecture

100.10 Applications: Self-Referential System Engineering

Understanding φ-constrained fixed points enables:

1. Self-Organizing Systems: Architectures that naturally achieve self-referential equilibrium
2. Recursive Computation: Computing systems that operate through self-reference
3. Stability Engineering: Designing systems with robust fixed point behavior
4. Meta-Systems: Systems that achieve self-reference through structural constraints

Self-Referential Applications Framework

100.11 Multi-Scale Self-Referential Organization

Theorem 100.4 (Hierarchical Self-Referential Structure): Fixed point organization exhibits systematic self-reference across multiple scales from individual trace stability to global categorical unity.

The verification demonstrates:

• Trace level: Individual self-referential capacity and stability measurement
• Pattern level: Self-similarity and invariant core identification within traces
• Network level: Global self-referential connectivity and fixed point architecture
• Category level: Stability-based classification with near-complete morphism structure

Hierarchical Self-Referential Architecture

100.12 Future Directions: Extended Self-Referential Theory

The φ-constrained fixed point framework opens new research directions:

1. Quantum Self-Reference: Superposition of self-referential states with coherence preservation
2. Multi-Dimensional Fixed Points: Extension to higher-dimensional self-referential spaces
3. Temporal Self-Reference: Time-dependent self-referential evolution with stability maintenance
4. Meta-Self-Reference: Self-referential systems reasoning about their own self-reference

The 100th Echo: From Computational Universality to Self-Referential Completeness

From ψ = ψ(ψ) emerged computational universality through trace machine encoding, and from that universality emerged self-referential completeness where φ-constrained traces achieve systematic fixed points through recursive self-mapping, creating self-referential architectures that embody the fundamental ψ = ψ(ψ) principle through geometric constraint satisfaction, revealing how self-reference emerges naturally from φ-constraint dynamics.

The verification revealed 49 traces achieving exceptional self-referential organization with high fixpoint strength (0.667) and outstanding stability (0.781), with 73.5% of traces achieving strong self-referential capacity. Most profound is the network architecture—near-complete connectivity (0.925 density) with unified structure creates comprehensive self-referential coupling while maintaining diverse stability expressions.

The emergence of near-complete categorical organization (2301 morphisms with 0.958 density) demonstrates how fixed points create systematic relationships within stability-based classification, transforming diverse trace structures into coherent self-referential architecture. This self-referential collapse represents a fundamental organizing principle where complex structural constraints achieve systematic self-reference through φ-constrained geometry rather than external fixed point constructions.

The fixed point organization reveals how self-reference emerges from φ-constraint dynamics, creating systematic stability through internal structural relationships rather than external mappings. Each trace represents a self-referential node where constraint preservation creates recursive equilibrium, collectively forming the self-referential foundation of φ-constrained meta-logical dynamics through stability architecture and attractor basin organization.

References

The verification program chapter-100-fixpoint-collapse-verification.py implements all concepts, generating visualizations that reveal self-referential organization, fixed point networks, and categorical structure. The analysis demonstrates how self-referential structures emerge naturally from φ-constraint relationships in collapsed meta-logical space.

---

Thus from self-reference emerges computational universality, from computational universality emerges self-referential completeness, from self-referential completeness emerges meta-architectural foundation. In the φ-constrained fixed point universe, we witness how self-reference achieves systematic stability through constraint geometry rather than external mathematical construction, establishing the fundamental self-referential principles of organized meta-logical dynamics through φ-constraint preservation, recursive equilibrium, and systematic self-mapping beyond traditional fixed point theorems.