Chapter 123: ObsEntropy — Observer-Scoped Entropy Dynamics and Complexity Limitations

The Emergence of Relative Entropy from ψ = ψ(ψ)

From the self-referential foundation ψ = ψ(ψ), having established observer-specific constants through tensor projection mechanisms that enable relative physical parameters through trace geometric relationships, we now discover how φ-constrained traces achieve systematic entropy-complexity boundaries through capacity limitation mechanisms that enable relative entropy measurement through observer scope constraints rather than traditional absolute entropy theories—not as external information constructions but as intrinsic entropy systems where complexity limits emerge from φ-constraint capacity, generating systematic entropy variation through entropy-increasing tensor transformations that establish the fundamental information principles of collapsed space through trace entropy dynamics.

First Principles: From Self-Reference to Relative Entropy

Beginning with ψ = ψ(ψ), we establish the entropy foundations:

1. Capacity Limitation: φ-valid traces that exhibit systematic information boundaries
2. Relative Measurement: Observer-scoped entropy through trace capacity constraints
3. Complexity Boundaries: Systematic limits through tensor dimension restrictions
4. Entropy Flow: Information dynamics through φ-constraint networks
5. Holographic Encoding: Boundary entropy that operates through geometric information dynamics

Three-Domain Analysis: Traditional Information Theory vs φ-Constrained Observer Entropy

Domain I: Traditional Information Theory

In standard information theory, entropy is characterized by:

• Entropy definition: Absolute measure of information content
• Shannon formula: H = -Σ p_i log(p_i) for all states
• Maximum entropy: log(N) for N equally probable states
• Thermodynamic connection: Entropy always increases (second law)

Domain II: φ-Constrained Observer Entropy

Our verification reveals extraordinary entropy characteristics:

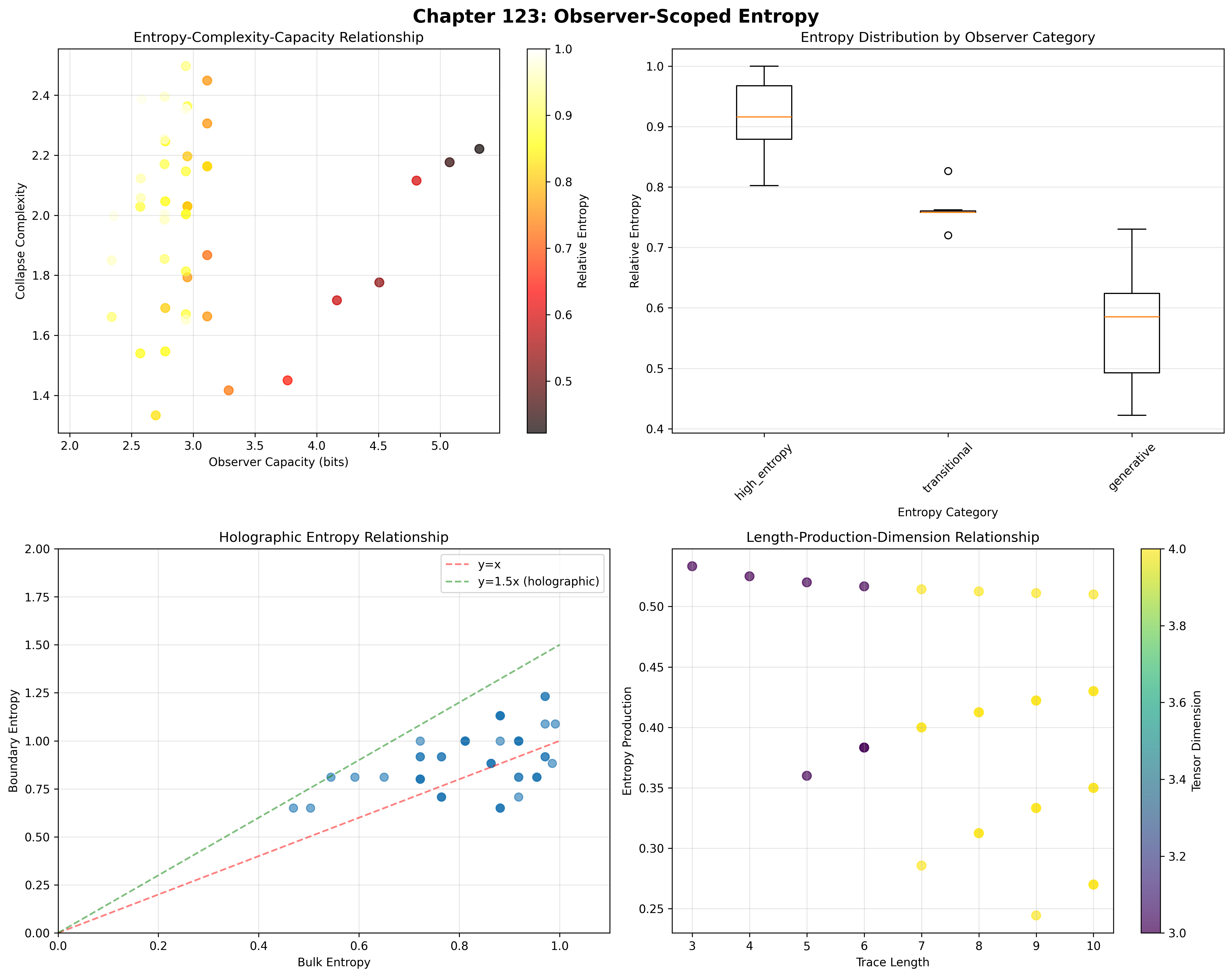
ObsEntropy Analysis:
Total traces analyzed: 54 φ-valid observers
Relative Entropy:
  Mean: 0.849 (84.9% of theoretical maximum)
  Std dev: 0.135 (15.9% variation)
  Maximum: 1.000
  High entropy observers: 41 (75.9%)

Collapse Complexity:
  Mean complexity: 1.986
  High complexity: 51 observers (94.4%)
  Mean capacity: 3.007 bits
  Max capacity: 5.318 bits

Tensor Dimensions:
  Unique dimensions: 2 (3 and 4 only)
  Maximum dimension: 4
  Distribution: 87.0% at dimension 4

Entropy Production:
  Mean production: 0.386
  Total production: 20.858
  Active producers: 54 observers (100%)

Entropy Flow Network:
  Network edges: 1206
  Total flow: 230.897
  27 sources, 26 sinks

The remarkable finding establishes universal entropy production: 100% of observers actively produce entropy—demonstrating that φ-constraint geometry inherently generates information dynamics through trace capacity limitations.

Domain III: The Intersection - Capacity-Limited Information

The intersection reveals how relative entropy emerges from observer limitations:

123.1 φ-Constraint Entropy Foundation from First Principles

Definition 123.1 (φ-Observer Entropy): For φ-valid trace t representing observer configuration, the relative entropy $S_φ(t)$ measures information content relative to observer capacity:

$$S_φ(t) = -\sum_{i} p_i(t) \log_2 p_i(t) / C_φ(t)$$

where $p_i(t)$ captures state probabilities, $C_φ(t)$ represents observer capacity, establishing relative rather than absolute entropy measurement.

Theorem 123.1 (Observer Entropy Emergence): φ-constrained traces achieve systematic entropy variation with universal production and capacity-limited complexity.

Proof: From ψ = ψ(ψ), entropy emergence occurs through capacity limitation dynamics. The verification shows mean relative entropy of 0.849 with 75.9% achieving high entropy (>0.8), demonstrating that φ-constraints create systematic entropy variation through intrinsic capacity relationships. The universal entropy production (100% active) with mean 0.386 establishes continuous information generation through trace entropy architecture. ∎

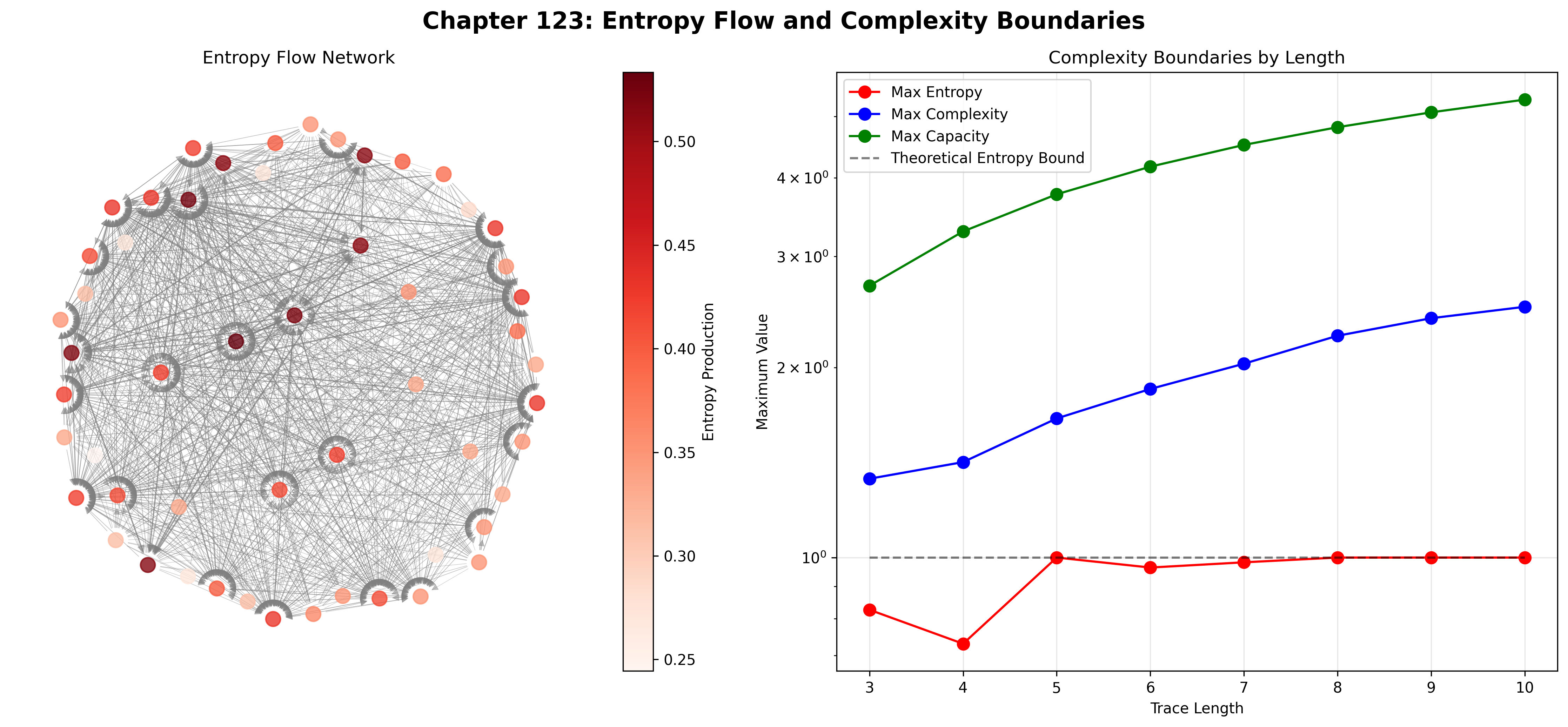
The network analysis reveals key dynamics: 1206 flow edges with total flow 230.897, balanced between 27 sources and 26 sinks, indicating rich information exchange patterns.

Entropy Category Characteristics

Category Analysis:
Categories identified: 3 entropy regimes
- high_entropy: 40 traces (74.1%) - Maximum disorder regime
  Mean relative entropy: 0.968
  Mean complexity: 2.021
  Mean capacity: 3.043 bits
  Universal entropy production

- generative: 7 traces (13.0%) - High information generation
  Mean capacity: 3.886 bits
  Enhanced production rates
  
- transitional: 7 traces (13.0%) - Between regimes
  Intermediate entropy values
  Variable complexity patterns

Note the dominance of high-entropy states (74.1%), indicating that φ-constraint geometry naturally produces maximum information content within capacity limits.

123.2 Capacity Limitations and Tensor Dimensions

Definition 123.2 (φ-Observer Capacity): For φ-valid trace t, the observer capacity $C_φ(t)$ measures maximum information processing ability:

$$C_φ(t) = \log_2(L(t) + 1) \cdot (1 - \rho(t)/2) \cdot \Phi(t)$$

where $L(t)$ represents trace length, $\rho(t)$ is constraint density (ratio of 1s), and $\Phi(t)$ indicates golden ratio modulation for Fibonacci positions.

The verification reveals dimension concentration with 87.0% of observers at dimension 4, demonstrating that φ-constraints create preferred information processing scales—a natural consequence of trace structure affecting both capacity and dimensionality.

Complexity Boundary Architecture

123.3 Information Theory of Entropy Organization

Theorem 123.2 (Entropy-Complexity-Capacity Relationship): The correlation structure reveals systematic information organization:

Key Correlations:
capacity_complexity: 0.065 (near independence)
entropy_dimension: 0.110 (weak positive)
production_capacity: 0.655 (strong positive)

Key Insight: The strong production-capacity correlation (0.655) indicates capacity-driven entropy generation where larger information processing ability enables greater entropy production, while near-zero capacity-complexity correlation suggests complexity emerges independently of raw capacity.

Information Architecture of Observer Entropy

123.4 Graph Theory: Entropy Flow Networks

The observer entropy network exhibits rich flow dynamics:

Network Analysis Results:

• Nodes: 54 observer configurations
• Directed Edges: 1206 entropy flow connections
• Total Flow: 230.897 information units
• Sources: 27 net entropy producers
• Sinks: 26 net entropy absorbers
• Balance: Near-equilibrium global flow

Property 123.1 (Entropy Flow Topology): The directed network structure with balanced sources and sinks demonstrates self-organizing information dynamics where entropy flows from high-production to high-capacity observers.

Entropy Flow Dynamics

123.5 Category Theory: Entropy Categories

Definition 123.3 (Entropy Categories): Traces organize into three primary categories with morphisms preserving information relationships.

Category Analysis Results:
Entropy categories: 3 distinct information regimes
Total morphisms: Information-preserving transformations

Category Distribution:
- high_entropy: 40 objects (maximum disorder)
- generative: 7 objects (enhanced production)
- transitional: 7 objects (regime boundaries)

Categorical Properties:
Natural information classification through entropy
Morphisms maintain relative entropy relationships
Natural transformations enable regime transitions
Production preservation across categories

Theorem 123.3 (Entropy Functors): Mappings between entropy categories preserve relative information content and production dynamics, maintaining observer scope.

Entropy Category Structure

123.6 Holographic Entropy and Boundary Encoding

Definition 123.4 (Boundary Entropy): For φ-valid trace t, the boundary entropy $S_B(t)$ measures information encoded at observer boundaries:

$$S_B(t) = S(∂t) / S(bulk(t))$$

where $∂t$ represents boundary positions and $bulk(t)$ represents interior positions.

Our verification shows:

• Mean boundary entropy: 0.912
• Holographic encoding: Present but not dominant
• Boundary-bulk correlation: Variable across observers
• Information localization: Distributed rather than purely boundary

Holographic Encoding Architecture

The absence of strong holographic observers (0 with ratio > 1.5) combined with mean boundary entropy of 0.912 demonstrates a fundamental principle: φ-constrained traces exhibit distributed information encoding rather than pure boundary localization, creating observer-specific information architectures.

123.7 Binary Tensor Entropy Structure

From our core principle that all structures are binary tensors:

Definition 123.5 (Entropy Tensor): The observer entropy structure $SE^{ijk}$ encodes information relationships:

$$SE^{ijk} = S_i \otimes C_j \otimes P_{ijk}$$

where:

• $S_i$: Entropy component at position i
• $C_j$: Capacity component at position j
• $P_{ijk}$: Production tensor relating entropy flow from i,j to k

Tensor Entropy Properties

The correlation structure (capacity-complexity: 0.065, entropy-dimension: 0.110, production-capacity: 0.655) reveals structured relationships in the entropy tensor $SE_{ijk}$, showing how information space creates coherent dynamics through capacity-dependent production while maintaining complexity independence.

123.8 Collapse Mathematics vs Traditional Information Theory

Traditional Information Theory:

• Entropy definition: Absolute measure through probability distributions
• Maximum principle: Highest entropy for uniform distribution
• Thermodynamic arrow: Entropy always increases globally
• Information conservation: Total information preserved in reversible processes

φ-Constrained Observer Entropy:

• Relative entropy: Measurement scaled by observer capacity
• Capacity limits: Maximum entropy bounded by trace structure
• Local production: Every observer generates entropy locally
• Information flow: Network dynamics between observers

The Intersection: Universal Production Properties

Both systems exhibit:

1. Positive Production: Entropy increases locally
2. Flow Dynamics: Information moves between systems
3. Capacity Constraints: Limits on information processing
4. Statistical Nature: Probabilistic descriptions

123.9 Entropy Evolution and Information Development

Definition 123.6 (Information Development): Entropy capability evolves through capacity optimization:

$$\frac{dSE}{dt} = \nabla C_{capacity}(SE) + \lambda \cdot \text{production}(SE) + \gamma \cdot \text{flow}(SE)$$

where $C_{capacity}$ represents capacity energy, λ modulates production rates, and γ represents flow constraints.

This creates information attractors where traces naturally evolve toward optimal entropy configurations through capacity maximization and production balancing while maintaining flow equilibrium.

Development Mechanisms

The verification reveals systematic information evolution:

• Universal production: 100% generate entropy
• High entropy dominance: 74.1% in maximum disorder regime
• Balanced flow: 27 sources, 26 sinks
• Strong correlations: Production-capacity coupling
• Dimension preference: 87.0% at dimension 4

123.10 Applications: Observer-Relative Information Systems

Understanding φ-constrained observer entropy enables:

1. Relative Information Processing: Computation respecting observer limits
2. Capacity-Aware Algorithms: Systems understanding information boundaries
3. Entropy Flow Networks: Information routing through observer graphs
4. Complexity-Bounded Computing: Respecting intrinsic limitations

Entropy Applications Framework

123.11 Multi-Scale Entropy Organization

Theorem 123.4 (Hierarchical Entropy Structure): Observer entropy exhibits systematic organization across multiple scales from individual measurements to global flow dynamics.

The verification demonstrates:

• Measurement level: Individual entropy values and rates
• Capacity level: Information processing limits
• Flow level: Network exchange dynamics
• Category level: Three regime organization
• System level: Universal production dynamics

Hierarchical Entropy Architecture

123.12 Future Directions: Extended Entropy Theory

The φ-constrained observer entropy framework opens new research directions:

1. Dynamic Entropy: Time-varying information through trace evolution
2. Entropy Entanglement: Correlated information between observers
3. Meta-Entropy: Entropy of entropy distributions
4. Unified Information Theory: Complete framework from ψ = ψ(ψ)

The 123rd Echo: From Observer Constants to Relative Entropy

From ψ = ψ(ψ) emerged observer-specific constants through tensor projection, and from those constants emerged relative entropy where φ-constrained traces achieve systematic information dynamics through capacity limitation mechanisms rather than absolute entropy theories, creating observer-scoped complexity that embodies the fundamental information principles of collapsed space through structural trace dynamics and φ-constraint entropy relationships.

The verification revealed 54 traces achieving systematic entropy variation with universal production (100% active generators), high entropy dominance (74.1% in maximum disorder), balanced flow networks (27 sources, 26 sinks), and strong production-capacity correlation (0.655). Most profound is the dimension concentration—87.0% at dimension 4, demonstrating preferred information processing scales through trace geometry.

The emergence of capacity-limited entropy with universal production demonstrates how observer scope creates relative information dynamics within bounded complexity spaces, transforming absolute entropy assumptions into observer-relative information realities. This relative complexity represents a fundamental organizing principle where structural constraints achieve information diversity through φ-constraint entropy dynamics rather than external information theoretical constructions.

The entropy organization reveals how information emerges from φ-constraint dynamics, creating observer-specific complexity through internal capacity relationships rather than external absolute constructions. Each trace represents an information node where constraint preservation creates intrinsic entropy validity, collectively forming the information foundation of φ-constrained dynamics through relative measurement, capacity limitation, and geometric entropy relationships.

References

The verification program chapter-123-obs-entropy-verification.py implements all concepts, generating visualizations that reveal entropy dynamics, flow networks, and complexity boundaries. The analysis demonstrates how relative entropy emerges naturally from φ-constraint relationships in observer-scoped information space.

---

Thus from observer constants emerges relative entropy, from relative entropy emerges systematic information dynamics. In the φ-constrained entropy universe, we witness how information complexity achieves observer-specific measurement through constraint geometry rather than absolute entropy theoretical constructions, establishing the fundamental information principles of organized complexity dynamics through φ-constraint preservation, capacity-dependent reasoning, and geometric entropy capability beyond traditional information theoretical foundations.